第3章:Prolog是如何回答问题的 - Learn Prolog The Hard Way

在上一章节里面，我给大家演示了一个Prolog特有的神奇的功能：它能够回答你提出的问题！在这一章里面，我将简单的解释一下Prolog是如何能够回答你的问题的。首先，还是自己试着把下面的程序写一下，然后加载到SWI-Prolog里面。

parent(di,yuqing).
parent(keyuan,jianbo).
parent(jianbo,di).

ancestor(X,Y):-parent(X,Y).
ancestor(X,Y):-parent(X,Z),ancestor(Z,Y).

然后我们问Prolog:

?- ancestor(keyuan,yuqing).

Prolog系统会试图证明这个查询，很显然，程序会返回”true.”那么，Prolog系统是如何找到答案的呢？当我们向Prolog提问”ancestor(keyuan,yuqing)”的时候，Prolog首先会在它的知识库里面寻找”ancestor”的定义，当然，它找到了两个”ancestor”的定义：

ancestor(X,Y):-parent(X,Y).
ancestor(X,Y):-parent(X,Z),ancestor(Z,Y).

按照默认的规定，它会首先取第一个规则：“ancestor(X,Y):-parent（X,Y).”由于这个规则里面的X,Y是变量，Prolog会给这两个变量赋值，使得：

ancestor(keyuan,yuqing) = ancestor(X,Y)

很显然，X=keyuan,Y=yuqing。之后，Prolog会把ancestor换成后面的条件：

ancestor(keyuan,yuqing) ==> parent(keyuan,yuqing).

之后，Prolog试图证明”parent(keyuan,yuqing)”,根据上面的程序，很显然，这是错的，会返回：”false”。那么，之后Prolog会怎么办呢？记得上面说过，ancestor有两个规则吧，我们之前根据惯例选择了第一个规则，现在我们可以试一下第二个规则：”ancestor(X,Y):-parent(X,Z),ancestor(Z,Y).”根据这个规则，Prolog会把”ancestor(keyuan,yuqing).”换成了：

parent(keyuan,Z),ancestor(Z,yuqing).

之前Prolog需要证明一个式子(ancestor(keyuan,yuqing).)，现在Prolog需要证明两个式子了。因为这两个式子中间是一个逗号，逗号的意思是”且“，所以只有当这两个式子都是”true”时候，整个的查询才是”true”。首先，Prolog会尝试第一个”parent(keyuan,Z).“它会在知识库里面找到：”parent(keyuan,jianbo)”。于是，Z=jianbo。这时候，我们之前的那两个式子变成了：

parent(keyuan,jianbo),ancestor(jianbo,yuqing).

然后，Prolog尝试证明第二个式子：”ancestor(jianbo,yuqing)”。同样的道理，Prolog首先找到的是：”ancestor(X,Y):-parent(X,Y)”，于是想证明”ancestor(jianbo,yuqing)”就变成了要证明”parent(jianbo,yuqing)”。很显然”parent(jianbo,yuqing)”会返回”false”。这时候，程序会试着把”ancestor(jianbo,yuqing)”替换成”parent(jianbo,Z1),ancestor(Z1,yuqing)”。要注意的是，此处我们不用Z作为变量了，而是用Z1作为变量，这叫做变量的重命名。原因是我们之前已经用过Z做变量了，为了把现在这个Z变量和之前的Z变量区别开来，我们把现在的Z变量重命名为Z1。很显然，无论变量的名字如何，它都是一个变量，理论上我们可以把它赋值成任何值，所以修改名字不会改变变量的含义。根据我们的知识库，此时Z1应该等于di。于是我们得到了两个式子：

parent(jianbo,di),ancestor(di,yuqing).

把”ancestor(di,yuqing).”换成”parent(di,yuqing)”，我们得到一个事实(fact),所以”parent(di,yuqing)”是真。综上所述，我们其实是用回溯的方式把”ancestor(keyuan,yuqing).”换成了：

parent(keyuan,jianbo),parent(jianbo,di),parent(di,yuqing).

由于上面的三个式子都是真的，所以”ancestor(keyuan,yuqing).”是真的。

下面这个图显示了Prolog是如何证明你的查询的：

"alt"

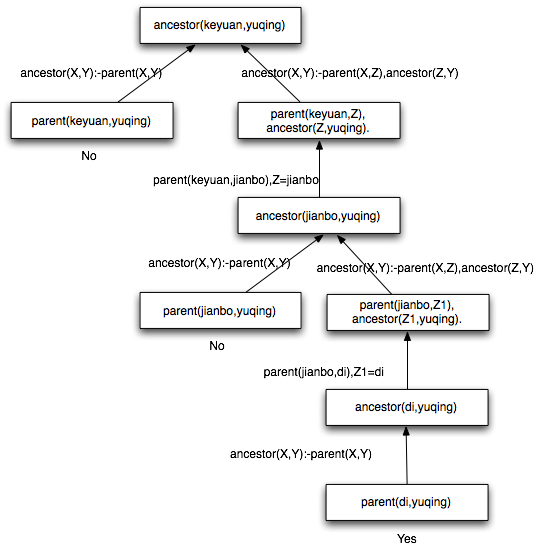
通过这个简单的例子，我们可以得出，Prolog通过三个方面来尝试着证明你给的查询(query)：

匹配(unifing/matching)。例如上面的”ancestor(keyuan,yuqing) = ancestor(X,Y)”，Prolog试图从它的知识库里面找出最符合你的查询的规则或者是事实。
变量重命名(variable renaming)。例如上面的”parent(jianbo,Z1),ancestor(Z1,yuqing)”，因为在同一个查询(query)里面已经有了”Z”，所以Prolog系统将重复的Z命名为Z1。(事实上，在Prolog内部，变量根本不会用”Z”,”Z1”这样的名字，Prolog的编译程序的时候就已经将”Z”换成了”G132329392049”这类名字以保证名字不会重复)。
回溯(back-tracking)。这是Prolog最最重要的一个特性。Prolog是用深度优先(depth-first search)的算法来寻找答案的。当一个规则或者是事实不符合时，Prolog会通过回溯的方式回到之前的状态，然后去尝试另外的规则或者是事实，知道你的查询(query)被证明为止。如果所有的可能性都搜索过了，你的查询仍然不能得到证实，那么Prolog会认为你的查询证实不了，返回”false”。有关回溯算法的详细介绍你可以去网络上搜索一下。

到这里，这一章就结束了，希望你对Prolog程序的执行顺序有了一个初步的了解。说实话，Prolog的程序回溯执行方式有时候我自己都想不明白，特别是遇到特别复杂的问题的时候。这个时候，最好的办法就是拿一张纸一支笔，亲自画一下程序的回溯图，就想上面的那个图一样，这样就能帮助你理解程序了～

加分习题

我们有如下代码：

parent(tom,bob). parent(pam,bob). parent(pam,liz). parent(pam,bob). male(tom). male(bob). female(liz). female(pam). sister(X,Y):-
```
 parent(Z,X),
 parent(Z,Y),
 female(X),
 X\=Y.
```
请比照着上面的教程里面”ancestor(keyuan,yuqing)”的执行顺序图画一个 ?-sister(liz,bob). 的执行图。(注：程序中的”X\=Y”是X不等于Y的意思)
(这道题有点难度哦)请看下图：

"alt"

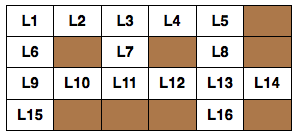
我们的目的是要在上面表格中白色的方格(带有LXX标识的方格)里面填上英文单词，可供选择的单词有：

word(d,o,g).    word(r,u,n).    word(t,o,p).    word(f,i,v,e).
word(f,o,u,r).  word(l,o,s,t).  word(m,e,s,s).  word(u,n,i,t).
word(b,a,k,e,r).    word(f,o,r,u,m).    word(g,r,e,e,n).
word(s,u,p,e,r).    word(p,r,o,l,o,g).  word(v,a,n,i,s,h).
word(w,o,n,d,e,r).  word(y,e,l,l,o,w).

试着写出一个规则solution.

solution(L1,L2,L3,L4,L5,L6,L7,L8,L9,L10,L11,L12,L13,L14,L15,L16).